Table of Content
Courses Taught
- Instructor:
- Teaching Assistant within Philosophy:
- Metalogic,
- Making Modern Science,
- Naturalised Epistemology,
- Introduction to Symbolic Logic,
- Introduction to Inductive Logic,
- Introduction to Logic (at the University of Warwick),
- Teaching Assistant outside Philosophy:
- Introduction to Linguistics (within Language Sciences),
- Introduction to Psychology (within Psychology),
- Grader:
- Making Modern Science,
- Introduction to Symbolic Logic.
Summary of Evaluations
Instructor Evaluations
| Introduction to Logic (School ave. in brackets) | Making Modern Science (School ave. in brackets) | Critical Thinking | |
| Overall Instructor Rating | 92.8% (80.8%) | 89.4% (81.4%) | 98.4% |
| Overall Course Rating | 81.4% (79.7%) | 83% (78.7%) | 94.4% |
| Course met objectives | 88.6% (81.4%) | 85.2% (81.8%) | 97.7% |
| Clarity of teaching | 90% (82.4%) | 87.5% (81.4%) | 96% |
| Responsiveness of instructor | 88.6% (83.1%) | 95.5% (82.5%) | 99.2% |
| Instructor encouraged interest and thought | – | 86.7% (79.4%) | 94.4% |
| Enthusiasm of instructor | – | 93.1% (84%) | 99.2% |
| Fairness of instructor | – | 89% (82.4%) | 97.7 |
| Instructor encouraged debate | – | 92.1% (78.4%) | – |
Teaching Assistant Evaluations
| Course | Teaching Effectiveness | School Average | ||
| Inductive Logic | 6.18 | 5.67 | ||
| Metalogic | 6.5 | 5.61 | ||
| Naturalised Epistemology | 6.13 | 5.61 | ||
| Symbolic Logic (S16) | 6.38 | 5.56 | ||
| Symbolic Logic (W16) | 5.65 | 5.58 | ||
| Average | 89% | 80% |
Selected Student Comments
Clarity of Exposition
I had never taken a philosophy class so I was nervous. I am glad I picked this one since it combined what I enjoy- the study of science- with history and philosophy. Professor Will was great about making thorough PPT presentations so the course material was clear and understandable. The topics covered were varied but extremely interesting. (Making of Modern Science)
Very good at explaining examples and simplifying them so anyone can understand. Hes super approachable and nice so asking for help, even during class which can be hard sometimes, is easy. (Critical Reasoning)
Will is an extremely friendly man. From the moment you see him, you know he’s approachable and helpful in anything you ask. His presentations are clear, his explanations make sense, and I think he’s very fair in terms of the work he gives out. (Critical Reasoning)
Discussion and Engagement
The teacher did an amazing job in incorporating class discussions in group and together that enforced positive engagement of opinions on the topics taught. (Making of Modern Science)
Will did a great job breaking down the ideas/concepts into understandable components. Having discussion during lecture was great to help digest ideas, see other views, develop our own views, and add interaction other than just listening to lectures. Extremely responsive professor and TA (Making of Modern Science)
He is extremely passionate and knowledgeable of the course materials. He is engaging with the students and will take personal interest in helping you improve in areas that he notices you struggling with. (Critical Reasoning)
I took this course just to fulfill my GE requirements and initially did not care much about it. Will made the class so engaging that I began caring about the material and began challenging myself to actually learn and apply the concepts instead of just remembering answers and definitions. (Critical Reasoning)
The professor did an extraordinary job working with students. He was available to do group sessions and individuals sessions. The course was well organized and structured. (Introduction to Logic)
Online
he was very responsiveness, always felt like he wanted to help so it made me feel comfortable asking him questions. Really appreciated the videos he made for extra practices. (Introduction to Inductive Logic)
All aspects were intellectually stimulating, including video lectures and online assignment and homework. (Introduction to Logic)
Full Evaluations
| Course | ||
| Winter 16 Symbolic Logic | Full | Summary |
| Spring 16 Symbolic Logic | Full | Summary |
| Fall 16 Naturalized Epistemology | Section 1, Section 2 | Summary |
| Spring 17 Making Modern Science | Missing | |
| Fall 17 Introduction to Linguistics | Full | Summary |
| Spring 18 Psych Fundamentals | Full | Summary |
| Fall 19 Introduction to Linguistics | Full | Summary |
| Winter 19 Metalogic | Full | Summary |
| Summer 19 Critical Thinking (Instructor) | Full | |
| Fall 19 Making Modern Science (Instructor) | Full | Summary |
| Spring 20 Inductive Logic | Full | Summary |
| Fall 20 Introduction to Logic (Instructor) | Full | Summary |
Sample Syllabi
Introduction to Logic (taught Fall 2020)
Abstract: Logic is the study of arguments. It seeks to sort these arguments into those that exhibit good reasoning and those that do not. In this course, we will develop tools to evaluate arguments in service of that end. The main focus of the course will be on the logic of formal languages, in particular the propositional and predicate calculi. We will focus in particular on translating between English claims and sentences and formal languages, on understanding the key logical concepts, and on the method of proof, which helps us identify good arguments. In doing so, we aim to better understand human reasoning in the world around us.
Text: The complete course can be viewed at carnap.io
Learning outcomes:
- Understand the formal languages of the propositional and predicate calculi, being able to translate between formal sentences and claims in natural language (English).
- Develop skills in deductive reasoning, using Fitch style proofs to explore the relation of logical consequence between different formal sentences.
- Constructing informal proofs.
- Understanding how work in logic goes beyond the simple systems normally taught.
Schedule:
Week 1 Introduction to Logic
Week 2 Introduction to Propositional Logic
Week 3 Deduction in Propositional Logic
Week 4 Formula Equivalence in Propositional Logic
Week 5 Introduction to First-Order Logic
Week 6 Semantics of First-Order Logic
Week 7 Deduction in First-Order Logic
Week 8 Deduction in First-Order Logic Continued
Week 9 Formula Equivalence in First-Order Logic
Week 10 Philosophy of Logic
Assessment: Weekly homework completed on carnap.io and a cumulative final exam also on carnap.io.
Narrative explanation: This course was designed for upper-division students most of who were majoring in philosophy or linguistics. It was taught entirely online during COVID. It was clear at that point that student absences were inevitable and so the course was designed with this in mind. I implemented a flipped classroom in which lectures were online pages on carnap.io interleaving text, videos, and interactive exercises. An example lecture is discussed below in the example materials section. The use of the site carnap.io also meant that student extensions could be managed easily and students could receive instantaneous feedback from the application before submitting work. The course covered the standard material for an introductory course but as an upper-division version additional materials were provided, such as some material on metatheory, and more difficult problems tackled.
Making of Modern Science (taught Fall 2019)
Abstract: While fulfilling a General Education requirement, this course will give students a better understanding of the history of science and introduce them to the difficulties in deciding what does and does not count as science using historical case studies. This course will allow science majors to more critically assess the historical narratives they are given about their subject and prepare all students to take upper division history and philosophy of science courses. You will be assessed by writing two essays and one exam. The first essay will demonstrate your ability to apply the theories of science we learned to historical case studies. The second will demonstrate your ability to research beyond the material of the course by asking you to discuss a little-known figure in the history of science. The exam will show your general mastery and memory of the course material.
Text:
Bowler, Peter J., and Iwan Rhys Morus. 2010. Making Modern Science: A Historical Survey. University of Chicago Press.
Godfrey-Smith, Peter. 2009. Theory and Reality: An Introduction to the Philosophy of Science. University of Chicago Press.
Learning outcomes:
- Understand the difficulties inherent in demarcating science.
- Analyse attempts to define science and evaluate them with the use of historic case studies.
- Learn about the history of modern science by looking at a series of historical case studies.
- Research cases of learning and people that aren’t part of the canon of history of science and evaluate how this work compares to theories of science and historical case studies.
- Learn about the impact science has had on society. Evaluate whether there is any way to distinguish between `bad’ science and other endeavours.
- Manage time, follow instructions,
- Engage in discussions in a respectful and constructive manner,
- Essay writing skills including citations and thesis writing,
- Critical analysis of texts,
- Giving clear and compelling arguments for your views, presenting objections to your views charitably and responding to objections robustly.
Schedule:
Week 1 Hypothetical Deductive Method Reading: Falsificationsim Ch. 4 in Theory & Reality
Week 2 Paradigm Shifts and Revolutions & Kuhn Ch. 5 & 9
Week 3 The Scientific Revolution Reading: Making of Modern Science (MMS) Ch. 1 & 2
Week 4 The Chemical Revolution Reading: MMS Ch. 3
Week 5 The Age of the Earth Reading: MMS Ch. 5
Week 6 Darwinism Reading: MMS Ch. 6
Week 7 20th Century Cosmology Reading: MMS Ch. 12
Week 8 Global History of Science Reading: Sciences and the Global, Sivasundaram 2010
Week 9 Science and Society: Biology and Racism Reading: Race, Empire, and Biology before Darwinism, Sivasundaram
Week 10 Science and Society: Medicine and Gender Reading: The Five Sexes, Fausto-Sterling 1993
Assessment: Weekly reading reflections, two essays and a final exam. The first essay was scaffolded with students submitting their sources, outline, draft, and peer review in the weeks leading up to the hand-in deadline.
Narrative explanation: This course had a large number of students majoring in history and philosophy and was cross-listed in both departments, as such it was important to ensure that the course balanced philosophical and historical material. This was achieved by teaching philosophy for the first 2 weeks before moving on to look at historical case studies for the next 5 weeks. The philosophical content was continued by using the case studies to assess the views in philosophy of science that had been covered in the first two weeks. The last 3 weeks looked at broader topics. Week 8 discussed science outside of the narrow tradition stemming from the scientific revolution. Week 9 and 10 then looked at ways that science interacts with social issues. Over half of the students were from STEM majors. This made it particularly important to help students develop skills in critical reading of texts and writing argumentative essays as these skills are not taught in the first few years of STEM degrees. To achieve this students were given a scaffolded essay, which is described below in the example materials.
Critical Reasoning (taught Summer 2019)
Abstract: The aim of this course is to train students to be able to assess arguments they encounter both formally and informally. Informal assessment will be taught by learning how to diagram arguments and identify fallacies in reasoning. Formal assessment will take the form of translating arguments into formal notation and then learning how to assess validity via truth tables, proofs, and Venn diagrams.
Text: Nolt, Rohatyn, and Varzi, Schaum’s Outline of Theory and Problems of Logic, McGraw Hill (2nd Ed.).
Learning outcomes:
- Diagram arguments.
- Translate informal arguments into formal notation.
- Check the validity of formal arguments using truth tables.
- Prove the validity of formal arguments using Fitch style proofs.
- Check the validity of categorical statements using Venn diagrams.
- Identify instances of 6 classes of fallacies.
Schedule:
Week 1 Tuesday: Diagramming arguments Ch. 1
Thursday: Translating to a formal language Ch. 3
Week 2 Tuesday: Truth tables Ch. 3
Thursday: Review
Week 3 Tuesday: First Test Proofs part 1 Ch. 4
Thursday: Proofs part 2 Ch. 4
Week 4 Tuesday: Categorical logic Ch. 5
Thursday: Venn diagrams Ch. 5
Week 5 Tuesday: Fallacies Ch. 2 and 8
Thursday: Review
Assessment: Weekly homework and two exams.
Narrative explanation: This was an intensive summer course where a 10 week schedule was compressed into 5 weeks. Most homeworks were done online using Carnap’s integrated quiz feature. Each class was three hours long. This made it vital to include exercise throughout the lectures, both to keep the student’s attention and to assess whether the class was ready to move on. A variety of team exercises proved very effective in remotivating students near the end of class.
Philosophy of Language
Abstract: This course covers traditional issues in the philosophy of language. This includes the sense and reference distinction, Russell and Kripke’s views on the meaning of names, speech acts, Greacian principles and Davidson’s theory of meaning. But it also looks to include work of interest to the intersection of linguistics and philosophy. This includes Chomsky’s views on innate language ability and Montague grammar.
Text: Hornsby, Jennifer & Longworth, Guy (eds.) (2005). Reading Philosophy of Language: Selected Texts with Interactive Commentary. Wiley-Blackwell.
Learning outcomes:
- Use a range of philosophical techniques to analyze and evaluate arguments.
- Present and defend a judgment orally in a group setting
- Acquaint students with some of the central issues in philosophy of language.
- Improve students’ skills in critical reading and critical thinking.
- Provide students with an intellectual foundation for future philosophical study within philosophy of language.
Schedule:
1 Words and images in Locke Reading: J. Locke, On Words (in textbook)
We consider an attractive naive view of the meaning of words, that their meaning is constituted by the images we associate with them. The problems we find here help motivate our move to theories such as Frege’s.
2 Sense and Reference Reading: G. Frege On Sense and Reference (in textbook); Selection from N. Salmon Frege’s Puzzle
We look at Frege’s distinction between sense and reference. Dummett’s suggestion of sense as a procedure for finding the reference is discussed as well as some modern attempts to formalise this idea. We then look at Salmon’s criticisms of the distinction.
3 Proper names Reading: B. Russell On Denoting; Selection from Kripke Naming and Necessity
We first set out Russell’s argument on denoting that proper names are abbreviated definite descriptions. We then consider Kripke’s criticism of this and attempts to give a more detailed picture of his causal historical theory of the meaning of names.
4 Ordinary Language Philosophy and its Critics Reading: J.L. Austin Performative Utterance (in textbook); R. Chisholm Philosophers and Ordinary Language
We consider Austin’s theory of speech acts and the larger movement of ordinary language philosophy. We turn to criticisms of the movement and its continued influence.
5 Pragmatics Reading: Grice Logic and Conversation; E. Borg On three theories of implicature: default theory, relevance and minimalism
We look at Grice’s theory of conversational implicature and use this as a starting point to look at contemporary theories of pragmatics.
6 Truth theories of meaning Reading: D. Davidson Radical Interpretation (in textbook); A. Gupta A Critique of Deflationism
We look at the suggestion that a theory of meaning should be given as a theory of translation from the object language to truth conditions in the metalanguage. We see how this has led to one of the most systematic attempts to offer a formal semantics for natural language. But we also look at the criticisms levelled at it.
7 Knowledge of Language (Essay due) Readings: M. Dummett What do I know when I know a Language? (in textbook); N. Chomsky Knowledge of Language as a Focus of Inquiry (in textbook)
We look at attempts to explain what knowledge of a language consists in. Turning first to solutions in philosophy, we move on to look at what linguistics has to tell us about this.
8 & 9 Montague Grammar Reading: notes on course website
We will introduce modal higher-order type theory through linguistic examples and show how this framework (which forms the basis of much modern formal semantics) deals with the sense reference distinction and proper names.
10 Formal Semantics and Philosophy Reading: B. Partee {\it Formal Semantics: Origins, Issues, Early Impact}
We have already seen how formal semantics can be used to help explicate notions like sense and reference but in the last week, we take a survey of how it can influence other philosophical questions.
Assessment: Weekly reading reflections, one essay, and one exam.
Narrative explanation: This proposed course would aim to give students a solid foundation in the philosophy of language allowing them to understand current debates. It would also aim to give them an understanding of the difficulties and achievements of the philosophy of language and a more sophisticated grasp of how language works. I have also aimed to include work on the border of linguistics and philosophy of language, as my background well places me to introduce students to this work and I believe it helps achieve a fuller understanding of how philosophy and linguistics together are developing a picture of how language works.
Proof Theory (graduate level)
Abstract: This course has two parts. In the first part, we show the equivalence of Hilbert, Gentzen and sequence calculi, as well as the equivalence of various modifications of the sequence calculus. We then show cut-elimination for the sequence calculus and normalization for the Gentzen system. This covers many of the foundational results in proof theory. In the second half of the course, we turn to more philosophically motivated projects in proof theory and look at Martin-Lof type theory and proof-theoretic semantics.
Text: A. S. Troelstra and H. Schwichtenberg. (2000) Basic proof theory. Second edition. Cambridge University Press, Cambridge.
Learning outcomes:
- Understand the difference between and construct proofs in Gc/i/m, Nc/i/m, and H–c.
- Be able to prove equivalence results between the different formal calculi.
- Understand the proof strategy for cut elimination and normalization.
- Have an understanding of how proof theory can be applied to philosophical problems.
- Find a research question and successfully self direct a project to attempt to answer the question.
Schedule:
Week 1 Three Logics and Three Systems
We introduce Gentzen natural deduction systems (G) and use this to define classical (c), intuitionistic (i), and minimal (m) logic. This gives us three systems Gc, Gi, and Gm. We then introduce the sequence calculus with structural rules, giving us the systems Nc, Ni, and Nm. A Hilbert system H–c is introduced for the universal, implication, negation fragment of classical logic.
Week 2 Equivalence of Gc/i/m with Nc/i/m
We will demonstrate that Gc is equivalent to Nc and similarly for i and m.
Week 3 Variants on the sequence calculus
We introduce N1 a variant on the sequence calculus with context sharing and N2 a variant with no structural rules. We prove that N1i and N2i are equivalent.
Week 4 Cut Elimination
We define N1– as the sequent calculus with context sharing but without cut. We prove that N1m is equivalent to N1–m. This result is called cut-elimination and is one of the foundational results of proof theory.
Week 5 Review and Midterm
Week 6 Normalization
We define reduction procedures in Gentzen systems and use these to prove normalization for Gm.
Week 7 Proof-Theoretic Semantics
We look at Prawitzes definition of proof-theoretic validity and discuss Dummett’s argument for Harmonious proof rules.
Week 8 lambda-calculus and the Curry Howard isomorphism
We introduce the lambda-calculus and then show the Curry Howard isomorphism between the implication fragment of minimal logic Gm and the lambda-calculus.
Week 9 Martin-Lof Type Theory
We will work through the rules for Martin-Lof type theory and demonstrate how they expand the Curry Howard isomorphism to the entirety of Gi.
Week 10 Philosophy and Type Theory
We discuss how proof-theoretic semantics motivated Martin-Lof type theory and look at the motivation behind the current Homotopy type theory project.
Assessment: Weekly homework and a project which would allow students to pick between writing an essay, completing a proof, or completing a coding project. A list of projects would be provided but students would be allowed to pick their own.
Narrative explanation: This is a graduate-level course on proof theory. It is aimed at students who have done a first course in logic but does not presume a more advanced background. It also aims to be accessible to students from related subjects such as mathematics and computer science. The course would introduce students to the most important results in proof theory in the first 6 weeks, namely the equivalence of various proof systems and the normalization and cut-elimination results. The next 4 weeks look at important topics in proof-theoretic semantics and type theory. This allows for more philosophically rich material to be presented and ensure that philosophy graduate students who are not as interested in technical work are fully catered for by the course.
Sample Course Materials
A Flipped Classroom
With the move to online teaching, I chose to flip my classroom. Instead of traditional lectures, I created pages on carnap.io integrating videos, text, and interactive exercises. The page discussed can be found here.
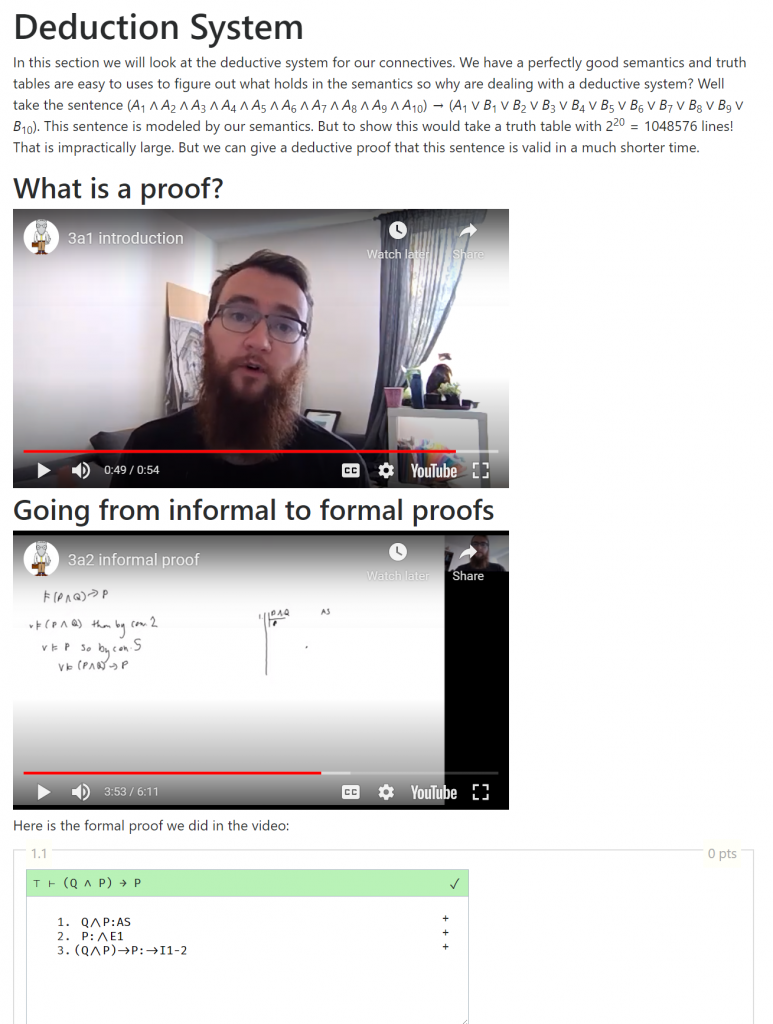
This is the beginning of the lecture. You can immediately see how text, videos, and exercises are integrated. After quickly motivating the topic of the lecture via the text paragraph, the students are given two short videos; one introducing the idea of proofs and another giving them their first example of a formal proof. After that, the proof from the video is presented in the interactive exercise environment.
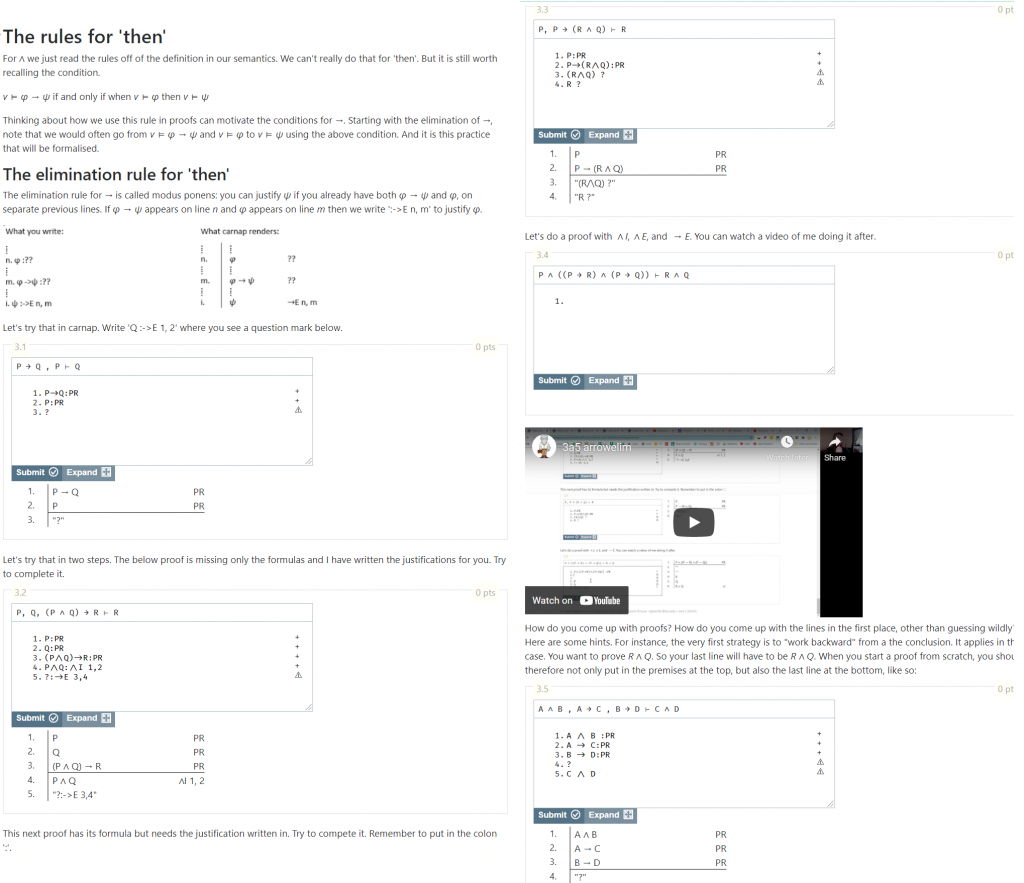
Below you see part of the lecture for the connective ‘then’. The informal explanation of the proof rule and the formal presentation of the rule is given in the text. Students are then given exercises of increasing difficulty. Exercise 3.1 starts by just asking the students to use the correct syntax for the interactive environment. While 3.2 and 3.3 give fill in the blank exercises of increasing difficulty. This means the students have seen 3 example proofs before being asked to construct a relatively simple proof themselves. A video is then used to demonstrate how the proof can be constructed. This demonstrates how the interactive environment can be used to scaffold students learning and introduce the necessary concepts step by step.
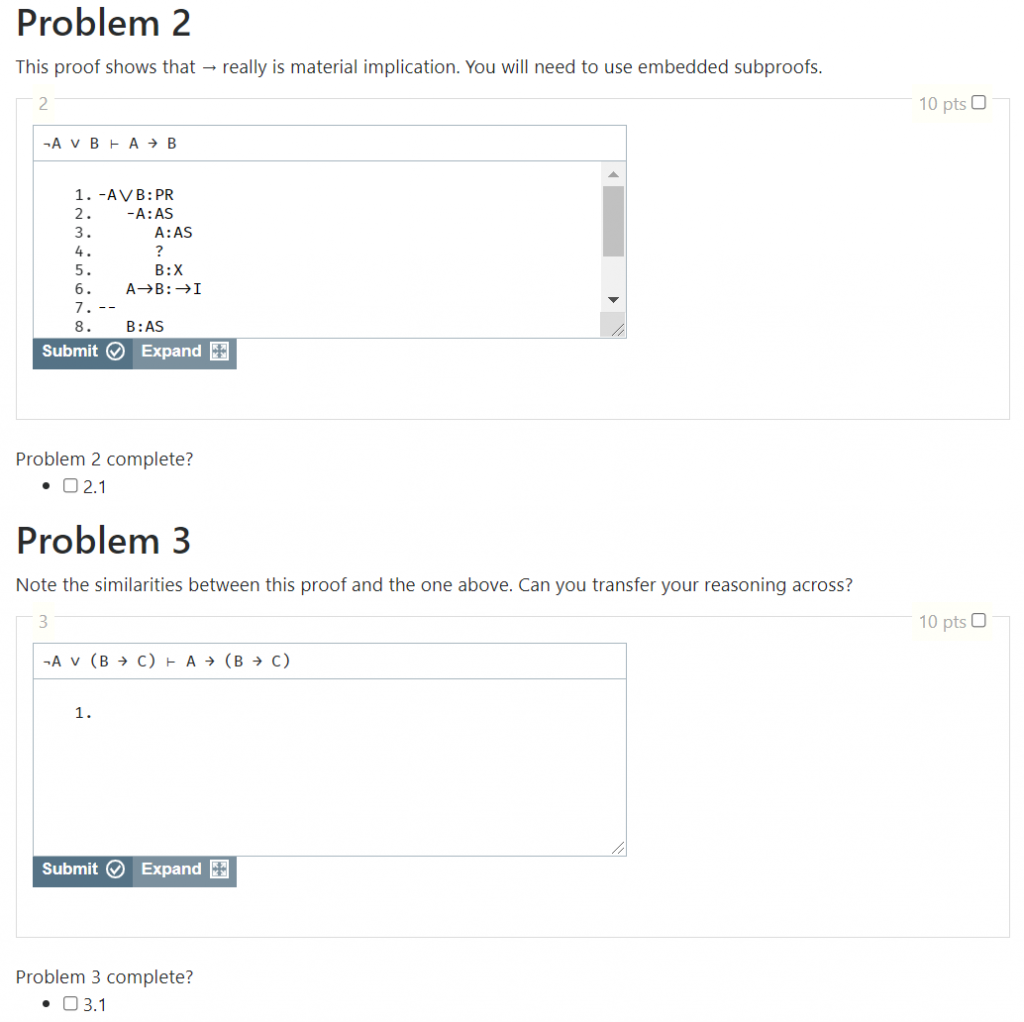
The lecture has prepared the students for the homework. As you can see on the right, homework problems used the same interactive exercise environment as the lectures. The scaffolded difficulty is also found in the homework where some problems are partially completed (as in problem 2), while others are left entirely to the students (as in problem 3).
A Scaffoled Essay Assignment
Students have different levels of experience with essay writing. Scaffolded assessments give students a framework to develop the skills needed to succeed in higher education. For my course, Making Modern Science, I developed the following scaffolded essay assignment.
The website contained a section on practical skills needed for essay writing such as citations and organization.
Time management is a major hurdle for students, so assignments were spaced out to ensure work on the essay happened over the course.
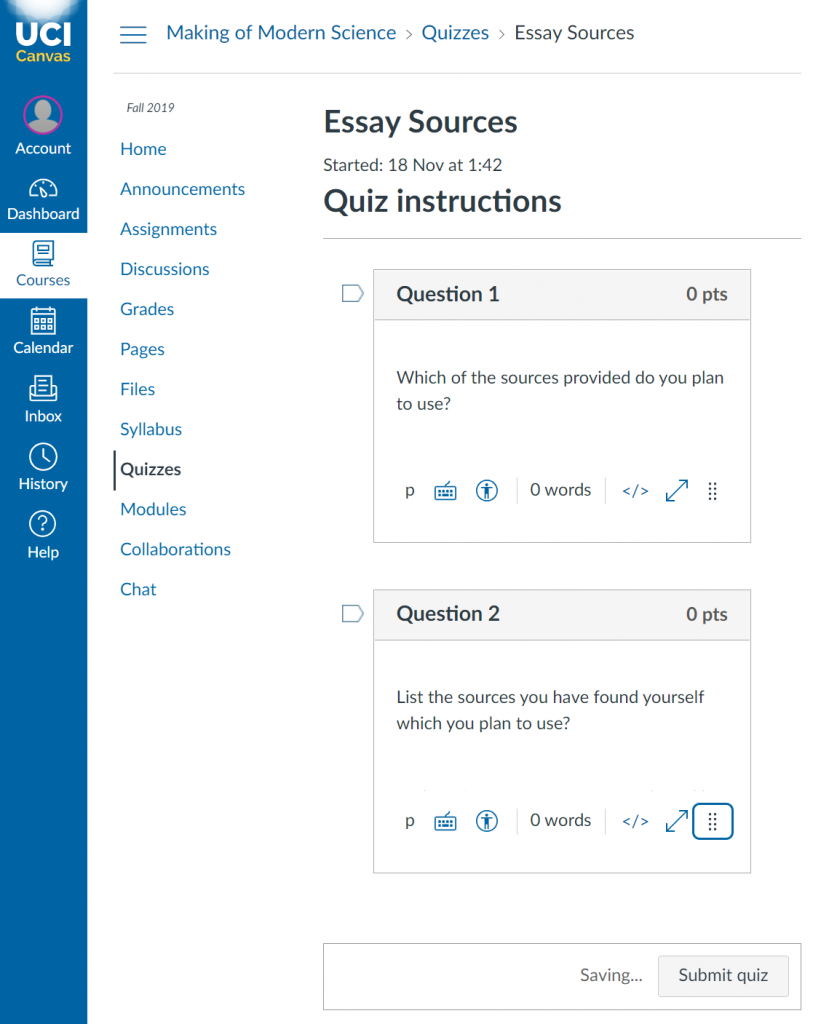
The first assignment was to submit a reading list. Students were given 10 possible sources for each essay and were asked to look at them and choose which ones they thought would be useful. They were also asked to find at least one source themselves.
This meant that all students were able to practice finding and evaluating sources. And the provided source lists helped guide students who lacked experiences such as those not majoring in the humanities and social sciences.
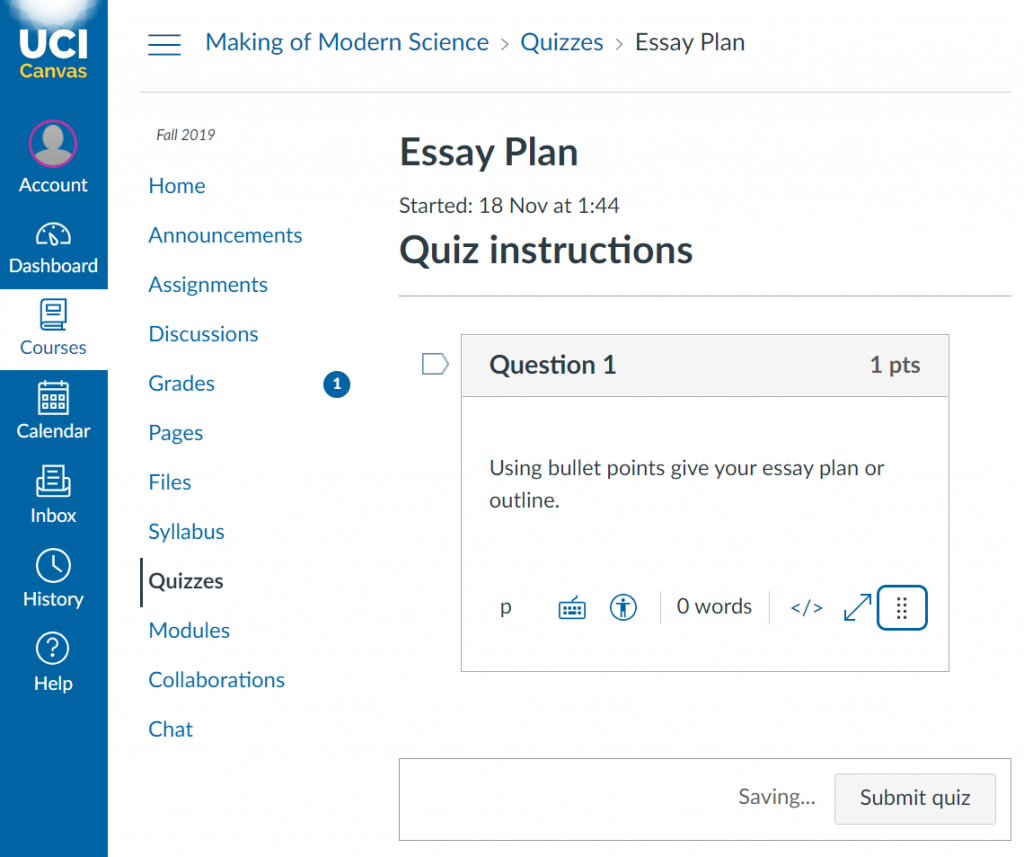
The second assignment was to complete an outline of the essay.
This assignment was given a week before the deadline for the draft. The aim was to help students develop the argument of their essay by requiring them to outline in bullet points. They had practised this exercise in sections the week before.
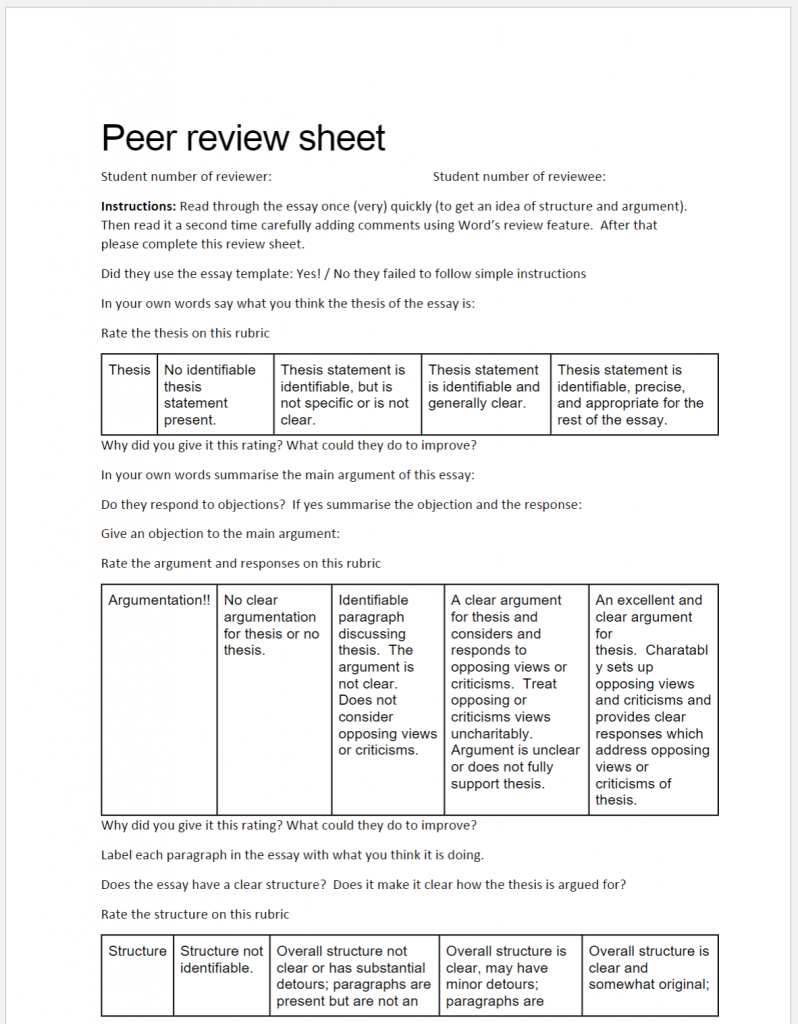
Students were then required to submit a draft two weeks before the final essay deadline. Using Canvas’s integrated peer review feature, students were paired up and gave feedback on each other’s essays. While able to give free form comments on the essay students were required to fill out a questionnaire to send to the other student.
This questionnaire took them through the grading rubric. The main aims of this exercise were to help students redraft their essays and to familiarise them with the rubric which was in turn designed to encourage working on the course learning outcomes.
Achieving Objectives through Lectures and Assessments
For my Making Modern Science course, one of the learning outcomes was to analyse attempts to define science and evaluate them with the use of historic case studies. Students were guided towards achieving this outcome by a combination of exercises in lectures and assessments.

The learning outcome was made explicit to students and the first essay questions asked them to argue whether a particular philosophy of science applied to a historical case study. One question was whether the scientific revolution constitute a paradigm shift.
The lectures gave the students the necessary information to assess this question. I made sure that students understood this by stating it explicitly.

Lectures contained active learning activities including minute essays, think-pair-share, class debates, and quizzes. I continually used these exercises to get the students thinking about whether the historical case study we were talking about related to a certain view in the philosophy of science.
By not giving answers but encouraging debate this helped students engage critically with the course. It also meant that students had notes on their own thoughts that could aid them in self-study.

The final exam contained a question where students had to evaluate the connection between a historical case study and a view in the philosophy of science. This was made clear to them in class, the revision guide and the practice exams.
The goal of this assessment was that by preparing for it students would have to think about whether the case studies provided evidence for or against certain views of science. As such studying would not just require memorisation but evaluation and so help them achieve the course goal.
